覆面算を解くポイント

---

　覆面算を解くのに、決まった方法があるわけではありません。しかし、いくつかの重要なポイントがあって、それを整理した上で、場合分けをすると、解きやすいことがあります。

　そのポイントとは、

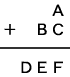
[1]　桁の繰り上がりに注目してください。

　　右図の場合、最上位が０(ゼロ)でないという約束がありますから、
　　Ｄ＝１，Ｅ＝０，Ｂ＝９，Ａ＋Ｃ＝Ｆ＋１０　となります。

[2]　加算部と和で、同じ桁に同じ文字があれば、両方を消すことができます。

[3]　数字の決まった文字を数字に置き換えて、式を整理します。

　具体的に、2001年8月の(2)を解いてみましょう。
問題を右に再録します。

[1]　繰り上がりに注目してください。

例題と同様に、た＝１、い＝０、お＝９ が決まります。
（お＝８　の可能性もありますが、その場合はう＝９となり、和の百位も９となって、百位の繰り上がりが２未満となり、成立しません）

[2]　十位に、加算部と和に　き　がありますから、両方を消します。

[3]　これを整理して経過図を示します。

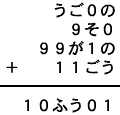
　各桁の計算は次のように整理されます。
　（N1:一位の繰り上がり　N3:百位の繰り上がりを表す）

一位

の＋の＋う＝１＋N1×１０

十位

そ＋１＋ご＋N1＝１０　（十位の繰り上がりは１に限定される）
そ＋ご＋N1＝９

百位

ご＋９＋が＋１＋１＝う＋N3×１０
ご＋が＋１１＝う＋N3×１０

千位

う＋９＋１＋N3＝ふ＋１０
う＋N3＝ふ

　以上のことから、場合分けをしていきます。

一位の計算	[残り]	十位の計算	百位の計算		千位の計算
の　う　N1		そ＋ご＋N1＝９	ご＋が＋11＝う	N3	う＋N3＝ふ
２　７　１	[3,4,5,6,8]	３＋５＋１＝９ ５＋３＋１＝９	５＋　＋11＝７ ３＋　＋11＝７		（不適） （不適）
３　５　１	[2,4,6,7,8]	２＋６＋１＝９ ６＋２＋１＝９	６＋８＋11＝５ ２＋　＋11＝５	２	５＋２＝７ （不適）
４　３　１	[2,5,6,7,8]	２＋６＋１＝９ ６＋２＋１＝９	６＋　＋11＝３ ２＋　＋11＝３		（不適） （不適）
５　１　１	（不適）
６　９　２	（不適）
７　７　２	（不適）
８　５　２	[2,3,4,6,7]	３＋４＋２＝９ ４＋３＋２＝９	４＋　＋11＝５ ３＋　＋11＝５		（不適） （不適）

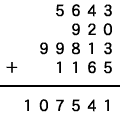
　ということで、の＝３、う＝５、そ＝２、ご＝６、が＝８、ふ＝７　残りの数字　４＝き　ということで、正解を見つけることが出来ました。