１−４．知恵の輪（チャイニーズリング）

[1]4連のチャイニーズリング

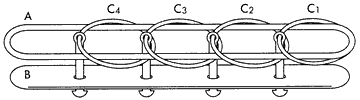
　チャイニーズ・リングと呼ばれる知恵の輪がある。これは[1]のように、細長い板Ｂに柄のついた環Ｃが数個（通常４から９個）はめこまれていて、これにＡのようなさおが通っている。このＡを取り外すパズルである。用具は飛騨の高山で民芸品として売られたほか、時折り輸入品が市販されている。
　中国には、古くから輪が九個のものがあり、九連環と呼ばれていた。材質は鉄か銅であったが、そのもとのものに石で作られた知恵の輪があった。中国の古い歴史の本『戦国策』の中に出てくる玉連環がそれだと言われている。話はこうである。

　戦国時代（紀元前403 〜 221）のことである。大国秦の昭王の使者が斉にやってきた。当時、斉では襄王が亡くなって、その后の君王后が政治を行っていた。使者は君王后に玉連環を献上してこう言った。
「斉には知恵者が多いと聞きました。ぜひこの環をはずしてみて下さい。」
　君王后は家臣の者に玉連環を渡したが、だれもはずすことができなかった。すると后は槌を取り寄せると、玉連環を打ち壊し、秦の使者にこう言った。
「謹んではずしましたよ」

[2]知恵の輪の紋

　九連環は、17世紀後半には、日本でもよく知られたパズルになっている。結構人気のあったことは、紋章に知恵の輪の紋[2]まであることでも知られよう。
　大数学者で、関孝和に対抗して最上流という一派を立てた会田安明は、数え年九歳（1755）のとき、人から九連環をもらった。父親に見せると、昔やったことがあると言って、三つ四つ輪をはずしたが、それ以上はできなかった。これだけはずせるのなら、理詰めで全部はずせるはずだと安明が言うと、父親はでは考えてみなさいと言った。それから安明は一晩寝ないで考え、とうとう知恵の輪の原理を解明した。彼はこれで自信を得て、数学の道へ進む決心をする。
　偉人のエピソードというものは後年の創作が多いが、この話は安明自身自叙伝の冒頭に書いているので、信用してよい。

　西洋では、イタリアのカルダーノが1550年に書いた本の中で論じているから、相当古くからあることがわかるが、中国との関係はよくわからない。その後イギリスのＪ．ウオーリスも論じている。注目すべきは、1872年にフランスのＬ．グロが二進法を利用してこの問題を巧みに解明したことである。
　チャイニーズ・リングを少しいじってみると分かるが、[1]の図で、一番右端の環は自由にはずせる。また二番目の環もはずすことができる。しかし、３番目から先は簡単にはいかない。一般にｎ番目の環は、（ｎ−２）番目の環までは全部はずれていて、（ｎ−１）番目の環がはまっているときに限ってはずすことができる。

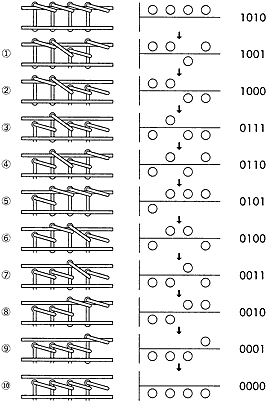
　ここでＬ．グロのやり方を簡単に説明しよう。まず横線を一本引いて、竿にはまっている環はその上部に、はずれている環はその下部に○印で表すことにする。この記載法で４連のものをはずす手順を図に示すと、[3]の中央のようになる。なお、一番端の、自由にはずせる環のある方を右に置いている。　ところで、

1. 横線より上にある○には、左から
   1､0､1､0､･･･と、交互に１と０をつける。
2. 横線より下にある○には、それより左側にはまっている環がなければ全部０、あればそれと同じ数字をつける。

という約束にすると、今の４連のものを解く過程は、[3]の右側のような二進法の数で表せることになる。
　この図でもわかるように、環を一個はずしたりはめたのする度に、この二進数が必ず増減する。したがって４連のものだと、全部はまっているときの1010から、全部はずれたときの0000にするには、その差だけの手数が必要になる。1010は十進数に直すと、

8 ＋ 0 ＋ 2 ＋ 0 ＝ 10

で10になる。0000は0であるから、けっきょく４連のものをはずすのに要する手数は10手ということになる。

[3]4連のもののはずす手順

　また、1010から順に１ずつ減らしていって、それをチャイニーズ・リングの配置に翻訳すれば、環をはずす手順を知ることができる。これにはちょっとしたコツが要るが、二進数を最高位から見ていって、

1. 最初に０が１個以上あれば、その個数だけはずれた環がある。
2. 最初に出てくる１は、必ずはまった環を示す。
3. 同じ数字が２個以上続く場合は、２個目から先は、はずれた環を示す。

といったことに注意すれば間違えずに翻訳できると思う。
　ｎ個の環をはずすのに要する最少手数は、したがって環が奇数の場合は（２ⁿ⁺¹ − １）／３手、偶数の場合は（２ⁿ⁺¹ − ２）／３手である。
　環の個数が４のものは10手だが、９連のもの（九連環）では341手、20連のものは699050となる。著者の持っている最大のものは36連である。これだとどうなるだろうか？