１−２６．四色問題

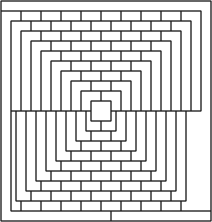
「地図に描かれた各国のうち、境界線を共有する２国は必ず異なる色で塗り分けるものとすると、最低何色の色が必要であろうか」という問題をいう。１点で接しているだけの２国や、全く接していない２国は、同色で塗って差し支えない。
　この問題は、A.ケーレイが1878年にロンドン数学会の席上で提起して以来、人々の注目を集めるようになった。
　塗り分けが３色では不十分であることは、[1]を見れば明らかだろう。また、５色あれば十分であることは、P.J.ヒーウッドが1890年に証明した。したがって、４色で十分かどうかの問題が最後に残ったことになり、この問題は「四色問題」と呼ばれるようになった。
　しかし、これが思ったほど簡単ではなく、専門の数学者のみならず、多くの町の研究家までがこの問題に熱中した。そして多くの証明が発表さたが、いずれも謝りがあったり、不十分であったりした。

　その間にハプニングも起こった。マーチン・ガードナーが、『サイエンティフィック・アメリカン』1975年 4 月号の「数学ゲーム」欄に載せた記事が原因だった。それは「なぜか世間の注意をひかなかった６つの衝撃の発見」と題するもので、その中に四色問題の話題も含まれていた。つまり、５色ないと塗り分けることのできない図形が見つかったという記事で、[2]のような図形が掲載されたのである。
　ガードナーはこの記事をエイプリルフールの冗談のつもりで載せたのだったが、これをまじめにとった読者が続出し、大変な騒ぎになった。実は[2]の図形はマクレガーがパズル用に作ったもので、用心して塗れば、４色で塗り分けが可能である。塗り分けの一例を[3]に示した。

　その後1976年に、イリノイ大学のウオルフガング・ハーケンとケネス・アッペルが大型コンピュータで1,200時間かけて、すべての図形が４色で塗り分けらることを証明し、この問題の決着をみた。

[1]3色で不十分な図の例

[2]マクレガーの問題

[3]塗り分けの一例

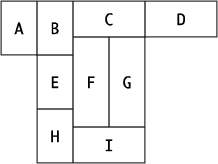
　最後にこれと関連した問題を考えて頂こう（[4]-A,B）。２人で交互に地図を１区画ずつ塗っていって、塗れなくなった方が負けというゲームがある。ただし、すでに塗っている区画と線で接している区画は塗ることができない。問題の図形で、先手が必ず勝つためには、どのように塗っていけばよいだろうか。

[4]-A

[4]-B