パズルの考え方・解き方(2) |
||||||
◆問題の本質をとらえるのが第一パズルを解くには、第一に問題の本質をとらえることが大切である。昔はやったなぞなぞに、こんなのがある。 問 ナポレオンはなぜ赤いずぼん吊りをしていたか。 「人はなぜずぼん吊りをするか」ならだれでも正解する。しかし、「人」が「ナポレオン」という特定の人物になり、ずぼん吊りに「赤い」という形容詞がつくと、とたんに答がわからなくなってしまう。これらの意味ありげな言葉に幻惑されてしまうからである。パズルの場合も同じで、与えられた条件から余計な要素を除いて、本質を見きわめることが大切である。 |
||||||
ひとつ実例を挙げよう。[6]の円の直径は何センチだろうか。長さのわかっているのは、BDが7センチ、ABが3センチということだけである。 |
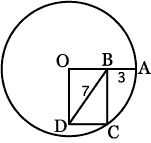 [6]円の直径は? 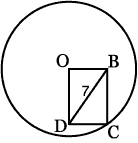 [7]余分なものを消すと |
|||||
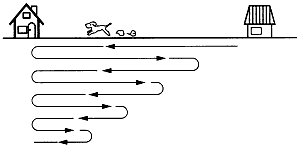
もう一つ例を挙げよう。太郎君は愛犬のポチを連れて4キロ離れた叔父の家へ出かけた。犬は行き先がわかったので、どんどん先に走って行って、叔父の家に着くとまた歩いている太郎君のところまで駆け戻って、再び叔父の家まで走って行く。ポチはこの動作を太郎君が叔父の家に着くまでくり返した。足の速さは太郎君が時速4キロ、ポチは16キロとすれば、犬は太郎君が叔父の家に着くまでに何キロ走っただろうか[8]。 この問題の本質は、太郎君が家を出てから叔父の家に着くまで、ポチは走り続けたということにある。それにさえ気がつけば、解決は容易だろう。時速4キロの太郎君が4キロ離れた叔父の家に到着するのに1時間。その間ポチの走った距離は16キロである。 |
||||||
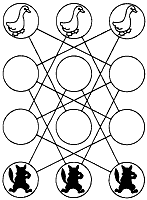
◆できるだけ単純化すること第二に必要なことは、できるだけ単純化するということである。その一つにデュードニーの言う「ボタンと糸法」がある。これが最も威力を発揮する入れ替え問題を例にとろう。[9]のようなゲーム盤の上の丸3箇所にガチョウのこまを置き、下の丸3箇所にキツネのこまを置く。この2種類のこまを交互に動かして、ガチョウのこまとキツネのこまをそっくり入れ換えるパズルがある。移動は直線の通路にそって行い、ガチョウがキツネに食べられないように、両者は必ず1個は間隔を開けねばならない。
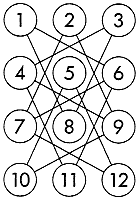
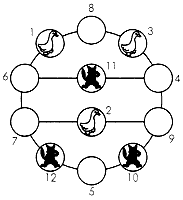
まず[10]のように、丸に番号をつける。丸をボタン、それをつなぐ直線を糸だとしてみよう。この糸を動かして全体を[11]のようにしても、もとの関係が保たれることは確かである。そこでこの図をもとにして解いていけば、ずっと容易に解くことができる。11のキツネと2のガチョウを円周に出すことを考えよう。まず10のキツネを5に、1のガチョウを8に移す。その上で11のキツネを6に、2のガチョウを9に移す。 パズルを解くのに広く利用できる独特の手法がある。これを自分のものとして、活用するのがよい。その一つに市松方式がある。
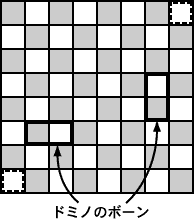
チェス盤は[13]のように市松模様に塗られている。これを利用することで、この問題は解決される。この上にボーンを縦に置いても、横に置いてもかならず白い目が1個、黒い目が1個覆われる。チェス盤には白、黒同数あるので、31個ボーンを置くと、最後に白い目と黒い目が各1個残ることになる。ところが右上隅と左下隅は同色なので、このような残し方はできないという結論になる。 |
||||||
他サイトへの無断転載はご遠慮ください。
●第1部・歴史的なパズル●
- 迷路
- リンド・パピルスのパズル(からす算)
- 魔方陣
- 知恵の輪(チャイニーズリング)
- ヨセフスの問題とまま子立て
- 渡船問題(川渡りの問題)
- 油分け算
- 盗人隠し
- さっさ立て
- 薬師算
- 碁石拾い
- おしどりの遊びと入れ替え問題
- 一小刀問題
- ねずみ算とフィボナッチ数列
- 知恵の板
- 虫食い算
- 目付け字と数当てカード
- 橋渡り問題と一筆書き
- ソリテア
- ハノイの塔
- デュードニー
- サム・ロイド
- 移動板パズル
- 図形消滅パズル
- パラドックス
- 四色問題
- チェスのパズル
- にせ金の問題
●第2部・言葉と絵のパズル●
- 回文
- アナグラム
- 折り句
- 暗号
- ダブレット(変形パズル)
- クロスワードパズル
- サーチワード、クリスクロス
- スクラブル
- 漢字作りパズル
- 単語作りパズル
- 判じ物と判じ絵
- 絵暦
- 新しい単語パズルの作り方
- 電卓文字遊び
- いろいろな文字遊び
- 絵当てパズル
- かくし絵
- さかさ絵
- その他の絵のパズル
●第3部・パズルの展開●
- ポリオミノ
- 立体パズル
- ブラックボックス
- 裏表パズル
- ザイルトリック
- 絵合わせパズル
- 切り継ぎパズル
- お菓子の分配
- クロスワードパズルの数字版
- 電卓数字パズル
- 覆面算
- 年賀用パズル
- コインのパラドックス
- マスターマインド
- パソコン・パズル
- 速算ダイス
- インスタント・インサニティ
- グラスパズル
- 匹見木のパズル