１−２８．にせがねの問題

　第二次世界大戦も終盤に近づいた1945年のことだった。『アメリカン・マセマティカル・マンスリー』１月号に次のような問題が提起された。出題者はバージニア州のE.D.シェルである。

　同種のコイン８枚と、てんびんが１台ある。コインのうち１枚はにせがねで、他のものより重さが軽い。てんびんを２回使うだけで、にせがねの存在を確認し、それを見つけだすことができるだろうか。

　この問題は大きな反響をまき起こした。解答は同誌の８−９月号に掲載された。この問題は、ちょっと考えると、まずてんびんの左右の皿に４枚ずつコインを載せて重さを比較し、どちらか軽い方の４枚を２枚ずつてんびんの左右の皿に載せて重さを比較する。最後に軽かった方の２枚を１枚ずつ両皿に載せて重さを比較して、軽い方がにせがねと結論される。しかしこのやり方では、３回測る必要がある。２回で済ますにはどうしたらよいだろうか。

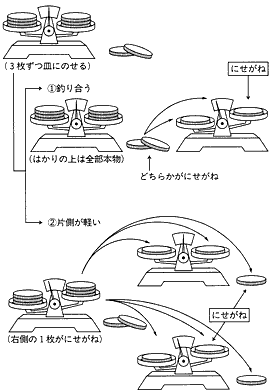
　正解を図で示すと、[1]のようになる。４枚ずつ測らずに、
（枚数＋１）÷３
枚ずつ、つまり３枚ずつ測るのが妙手である。このようにすると、Ｎ枚のコインがあって、Ｎが

3^n-1 ≦ N ＜ 3ⁿ

である場合は、ｎ回の測定でにせがねを見つけだすことができる。ただし、にせがねが混ざっていることが確実で、その確認をする必要がなければ、Ｎが

3^n-1 ＜ N ≦ 3ⁿ

のときにｎ回の測定でにせがねを指摘することが可能である。

　このにせがねの問題は、多くの数学者やパズル愛好家を熱中させた。そしてこの問題をさらに一般化した形の「コイン12枚の問題」が考え出されて『スクリプタ・マセマティカ』誌に発表された。その過熱ぶりは相当なものであったらしく、ドイツの潜水艦を沈めるために使われるべき多くの頭脳が、このパズルのために消費されたと書かれているほどである。
　コイン12枚の問題は、次のようなものである。

　見かけは全く同じコインが12枚あるが、そのうち１枚はわずかに重さが異なっている。その重いか軽いかを知らずに、３回てんびんを使うだけでそのコインを指摘するには、どうしたらよいだろうか。

[1]コイン８枚の問題の解き方

[2]コイン12枚の問題の解き方

　この問題の解き方を[2]に示した。一般にＮ枚のコインがあって、Ｎの値が

(3^n-1 - 1)／2 ≦ N ＜ (3ⁿ - 1)／2

のときにｎ回の測定でにせがねを確認することができる。