１−５．ヨセフスの問題とまま子立て

　人を円形に並ばせて、何人目かにあたった者を順に除いていくパズルを、西洋ではヨセフスの問題とよんでいる。これは370年ころ、ヘゲシッパスの名で書かれた次のような物語による。

　昔、ユダヤ人がローマに反抗して独立戦争を起こした。ユダヤの総司令官ヨセフスは、ヨタパタの町に篭城したが、ローマ軍に包囲されて陥落、仲間40人と共にほら穴に隠れた。ヨセフスと彼の友人は、なんとか生き延びたいと思っていたが、他の者は自決を望んだ。いよいよ集団自決をする段になって、ヨセフスは全員を円形に並べ、三番目ごとにほかの同士に殺してもらい、最後の一人は自殺をするという方法を提案した。これが認められたので、得たりとばかりヨセフスと友人は16番目と31番目に位置し、二人して九死に一生を得たという。

　ここに出てくるヨセフスは、歴史家として知られるフラウィウス・ヨセフス（37頃〜100頃）のことで、この出来事の大筋も彼の著した『ユダヤ戦記』にあり、実話を基にして作られた話である。

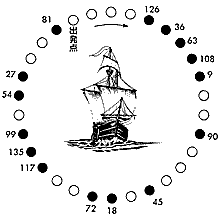
　ヨセフスの問題で最も有名なのは「トルコ人とキリスト教徒」の問題である。これも11世紀ころの写本にも見られるというほど古いパズルである。

　キリスト教徒15人、トルコ人（異教徒）15人が乗り合わせた船が暴風にあって難破し、15人を海に投じなければ沈没は免れない事態となった。そこで、船長は全員を円形に並べ、九番目、九番目にあたる者を、順に海に投じた。このとき、船長は[1]のように並べた。白丸がキリスト教徒、黒丸がトルコ人である。そのために、キリスト教徒は全員救われたのである。

[1]トルコ人とキリスト教徒の問題配置図

　このヨセフスの問題の日本版が「まま子立て」である。まま子立ては吉田光由の著した『塵劫記』（寛永８年版、1631）によればこうである。

　子供を30人持った母親がいたが、子のうち15人は実子、15人はまま子だった。ある日、母親はこの子らを円形に並べ、十番目、十番目にあたる者を順に除いていって、一番最後に残った者にこの家を継がせると申し渡した。いざ数えてみると、まま子ばかりが除かれていき、このままだと最後の一人も除かれることになった。そこでその子は、「これではあまりにも不公平です。こんどは私から数え始めて下さい」と言った。言い分がもっともなので、母親がその通りにすると、今度は実子ばかり除かれて、結局まま子が最後に残ったという。

[2]まま子立て配置図

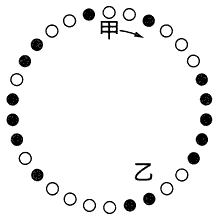
　この配列を[2]に示す。白丸が実子、黒丸がまま子を表しており、甲が数え始めの位置を、乙が最後に残ったまま子の位置を示している。
　わが国のまま子立ては吉田兼好（1283〜1350）の『徒然草』にもその名が出てくる。一説には藤原通憲の作ともいう。数え直しのある点が西洋のものと違っている。