１−２１．デュードニーのパズル

　ヘンリー・アーネスト・デュードニー（1857〜1930）は、イギリスの生んだ最大のパズリストである。小さい時からパズルが好きで、９歳のときにパズルの問題を作って少年雑誌に投稿し、賞金を貰っている。1890代にはイギリスの雑誌『ティット・ビッツ』（Tit-Bits）のパズル欄を担当して成功を収め、後に『ウイークリー・ディスパッチ』紙や『ストランド・マガジン』誌のパズル欄を担当した。
　彼の著書の中で特に有名なのは1917年に出版した『数学遊戯』（Amusements in Mathematics)で、パズル愛好家のバイブルとされた。わが国でもダイヤモンド社から『パズルの王様』の題で訳が出ている。
　デュードニーの創案したパズルはおびただしい数に上がっているが、特に優れたものをいくつか紹介しよう。

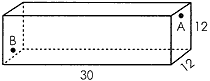
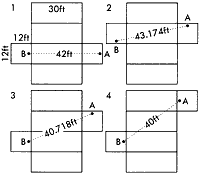
　[1]は「クモとハエ」で、長さ30フィート、幅12フィート、高さ12フィートの部屋の図である。一方の壁の中央、天井から１フィートの所Ａにクモがおり、向かい側の壁の中央、床から１フィートの所Ｂにハエがいる。クモがハエの所まで行く最短距離は何程だろうか。
　この問題は、展開図で調べた方がいい。ちょっと考えると、最短距離は[2]の１のコース（42フィート）のように思えるが、実際に計算してみると、最短コースは４（40フィート）である。このコースでは、クモはなんと部屋の６面のうちの５面を通ることになる。

[1]クモとハエ

[2]展開図による検討

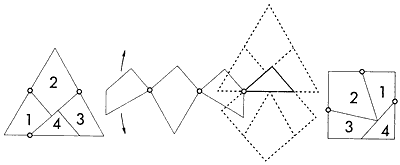　デュードニーは、切り継ぎ問題でも優れたやり方をいくつも発見しているが、中でも傑作なのは、正三角形を４つに切って並べ替え、正方形を作る[3]の解である。このやり方では、４つの片の３箇所をハトメでつないで、一端を固定し、もう一端を持って回していけばお互いの変換ができるというみごとなものである。

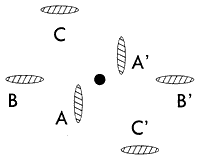
　もう一つ、彼の「葉巻のパズル」を紹介しよう。２人の男が四角いテーブルに座る。そして交互にテーブルの上に葉巻を置いていくが、葉巻がほかの葉巻に触れたり、テーブルから落ちたりしなければ、どんな置き方をしてもいい。２人が最善を尽くした場合、最後に葉巻を置くことに成功するのは、先手だろうか、それとも後手だろうか。
　答は先手である。先手はまず１本目の葉巻をテーブルの真ん中に立てる。あとは後手がテーブルのどこにどう葉巻を置こうが、常にそれと対称位置に葉巻を置いていけばよい（[4]）。後手の置いた場所の対称位置には必ず先手が置くことができ、手詰まりになるのは後手の方である。

[4]葉巻のパズル