このコーナーは、高木茂男氏の著書「パズル遊びへの招待」(発行:PHP研究所・1994年)の内容に著者自身が加筆・修正を加えたものを、著者本人及び出版元の許諾により掲載しているものです。
他サイトへの無断転載はご遠慮ください。
他サイトへの無断転載はご遠慮ください。
●第1部・歴史的なパズル●
- 迷路
- リンド・パピルスのパズル(からす算)
- 魔方陣
- 知恵の輪(チャイニーズリング)
- ヨセフスの問題とまま子立て
- 渡船問題(川渡りの問題)
- 油分け算
- 盗人隠し
- さっさ立て
- 薬師算
- 碁石拾い
- おしどりの遊びと入れ替え問題
- 一小刀問題
- ねずみ算とフィボナッチ数列
- 知恵の板
- 虫食い算
- 目付け字と数当てカード
- 橋渡り問題と一筆書き
- ソリテア
- ハノイの塔
- デュードニー
- サム・ロイド
- 移動板パズル
- 図形消滅パズル
- パラドックス
- 四色問題
- チェスのパズル
- にせ金の問題
●第2部・言葉と絵のパズル●
- 回文
- アナグラム
- 折り句
- 暗号
- ダブレット(変形パズル)
- クロスワードパズル
- サーチワード、クリスクロス
- スクラブル
- 漢字作りパズル
- 単語作りパズル
- 判じ物と判じ絵
- 絵暦
- 新しい単語パズルの作り方
- 電卓文字遊び
- いろいろな文字遊び
- 絵当てパズル
- かくし絵
- さかさ絵
- その他の絵のパズル
●第3部・パズルの展開●
- ポリオミノ
- 立体パズル
- ブラックボックス
- 裏表パズル
- ザイルトリック
- 絵合わせパズル
- 切り継ぎパズル
- お菓子の分配
- クロスワードパズルの数字版
- 電卓数字パズル
- 覆面算
- 年賀用パズル
- コインのパラドックス
- マスターマインド
- パソコン・パズル
- 速算ダイス
- インスタント・インサニティ
- グラスパズル
- 匹見木のパズル
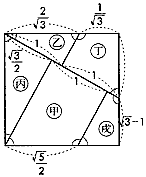
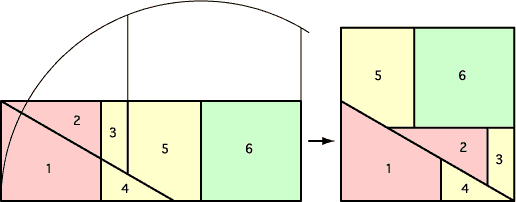
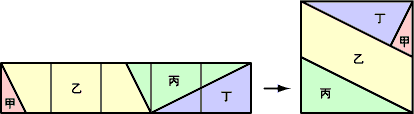
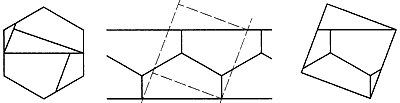
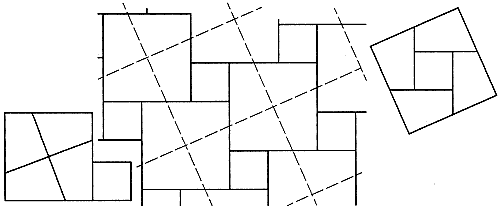
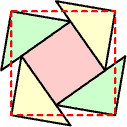 これに似た試みは、西洋でも古くから行われていて、10世紀ペルシアのアブル・ウェファは、3個の正方形を9片に切って、正方形にしている。
これに似た試みは、西洋でも古くから行われていて、10世紀ペルシアのアブル・ウェファは、3個の正方形を9片に切って、正方形にしている。