３−１３．コインのパラドックス

　与えられた図形の中に何枚のコインが詰められるかという問題は、一見非常に簡単そうに見えて、奥の深いものがある。その１つの問題を紹介しよう。

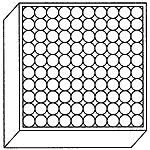　コインの直径を１として、10×10の箱にコインを重ならないように並べたら、最大何枚並べられるだろうか。次のように並べれば、むろん100枚並ぶ。これが最大だろうか。たいていの人はそうだと思うだろう。ところが違うのである。
コインを10行10列に並べたもの

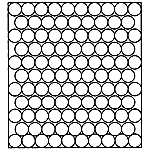　１段目はふつうに10個並べる。その上のコインは、コインとコインの間に置くようにする。こうすると一列に９個しかおけないが、高さは低くなる。その上はふつうに10個並べ、その上は９個、というように詰めていくと、次のように11段になって、けっきょく105個詰めることができる。
105個詰める並べ方

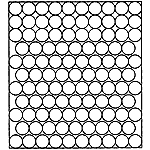　しかし驚くのはまだ早い。その上があるのだ。2つの並べ方を適当に混ぜると、次のようにもう１つ余計に置くことができる。つまり全部で106個である。
106個詰める並べ方

　今度は、コインを用いた錯視の例を紹介しよう。まず、１円玉を１枚と10円玉を15枚から20枚用意する。机の上に１円玉を置き、10円玉を相手に渡して、１円玉の直径と同じ高さになったと思うまで、10円玉を積み上げてもらうのである。たいていの人は、８枚か９枚積んだところで、これで等しくなったと思う。とこらが、実際は13枚積んで、やっと等しくなる。ひとつ試してみるとよい。

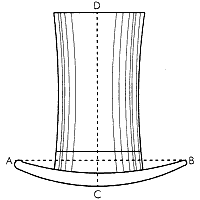　これはおそらく「シルクハットの錯視」と呼ばれている有名な錯視と、関係があるに違いない。右の図を見て頂きたい。このシルクハットの高さ（ＣＤ）は、その縁の幅（ＡＢ）より長く見えるが、実際はまったく等しい。われわれの目が横についているため、縦方向より横方向に目を動かしやすいことに原因があると考えられる。

　もう一つ、こんな問題はどうだろうか。紙に一円玉と同じ大きさ（直径が2.00cm）の穴を開ける。さてこの穴に、10円玉（直径が2.35cm）を通したいのだが、それは可能だろうか。可能とすれば、どうすればよいだろうか。むろん板のような硬質なものでは通るわけはないが、紙や布のような柔軟なものなら、これは可能である。やり方を次に示した。紙を２つ折りにして、まず、10円玉を通るだけとおし、軽く押しつけながら紙を矢印の方向に歪めると、10円玉はスルリと抜ける。実際にやるとよくわかると思う。

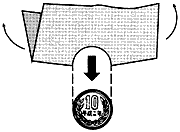10円玉の通し方