3−10.電卓数字パズル |
第2部の「電卓数字遊び」で電卓数字が文字遊びに使われた話をしたが、この形は数字のパズルでも当然注目されている。まず、次のパズルはどうだろうか。 電卓数字だと0,1,2,5,8は、さかさまから見ても全く同じ形をしている。では、1から99までのうち、この数字で表して、さかさまにしても変わらない数はいくつあるだろうか。この答は文の最後に述べるが、まず少し考えてみて頂きたい。
筆者は、この電卓数字をマッチパズルに利用することを考えた。マッチパズルには、次のようにローマ数字を使ったパズルが数多くある。
しかし、ローマ数字は最近ではなじみの薄いものになってしまった。そこでこれを電卓数字に変えてみたのだが、やってみると、従来不可能だったかけ算の問題も作ることができ、論理的に解ける問題ができるなど、新たな魅力があることがわかった。次の問題は1978年に筆者が作った第1作で、従来のマッチパズルが、大部分マッチ棒を動かすものであったので、マッチ棒の数を増減する形にしてみた。 マッチ棒で掛け算の式を作りました。ところが、だれかがいたずらをして、その式からマッチ棒を5本取り去り、図のようにしてしまいました。元の数はどうなっていたのでしょうか。数字の表し方は[1]によるものとします。
この問題の解き方であるが、まず乗数の7に注目する。これのもとの形はやはり7であるか、それに2本のマッチ棒を加えた9、あるいは3本加えた8のどれかである。被乗数の6は、もともと6だったか、8だったかのどれかである。積の1位も2か8のいずれかである。それから可能な組み合わせを選ぶと、次のようになる。 □6×7=□□2 被乗数の9は、もともと9であったか、これに1本加えた8かどちらかである。そこで最終的に検討すべきなのは、次の6種である。 (ア)86×7=602 このうち(ア)から(ウ)までの式の積は、もとの式の積752からは変換できないので、まずこれが除かれる。また、(エ)の式にするには、もとの式に6本足さねばならず、(カ)の場合は8本を要するので、この2つも除かれ、(オ)だけが残る。したがって解は次のようになる。
ところで、冒頭の問題の正解は10個である。つまり、 |
他サイトへの無断転載はご遠慮ください。
●第1部・歴史的なパズル●
- 迷路
- リンド・パピルスのパズル(からす算)
- 魔方陣
- 知恵の輪(チャイニーズリング)
- ヨセフスの問題とまま子立て
- 渡船問題(川渡りの問題)
- 油分け算
- 盗人隠し
- さっさ立て
- 薬師算
- 碁石拾い
- おしどりの遊びと入れ替え問題
- 一小刀問題
- ねずみ算とフィボナッチ数列
- 知恵の板
- 虫食い算
- 目付け字と数当てカード
- 橋渡り問題と一筆書き
- ソリテア
- ハノイの塔
- デュードニー
- サム・ロイド
- 移動板パズル
- 図形消滅パズル
- パラドックス
- 四色問題
- チェスのパズル
- にせ金の問題
●第2部・言葉と絵のパズル●
- 回文
- アナグラム
- 折り句
- 暗号
- ダブレット(変形パズル)
- クロスワードパズル
- サーチワード、クリスクロス
- スクラブル
- 漢字作りパズル
- 単語作りパズル
- 判じ物と判じ絵
- 絵暦
- 新しい単語パズルの作り方
- 電卓文字遊び
- いろいろな文字遊び
- 絵当てパズル
- かくし絵
- さかさ絵
- その他の絵のパズル
●第3部・パズルの展開●
- ポリオミノ
- 立体パズル
- ブラックボックス
- 裏表パズル
- ザイルトリック
- 絵合わせパズル
- 切り継ぎパズル
- お菓子の分配
- クロスワードパズルの数字版
- 電卓数字パズル
- 覆面算
- 年賀用パズル
- コインのパラドックス
- マスターマインド
- パソコン・パズル
- 速算ダイス
- インスタント・インサニティ
- グラスパズル
- 匹見木のパズル
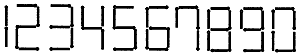 [1]電卓数字(マッチ棒による)
[1]電卓数字(マッチ棒による)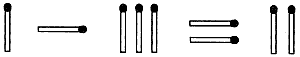
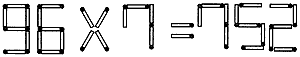
 [4] [3]の解答
[4] [3]の解答