3−5.ザイルトリック |
|
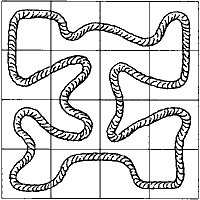
1977年5月、パズル懇話会の例会で「パズル玩具セミナー」を催した。その時、芦ヶ原伸之がドイツの「ザイルトリック」という玩具を紹介した。これは次の図のように16枚の正方形の板にロープ(ザイル)の絵が描かれたもので、それを4×4の正方形に並べて、全部のロープが1つの輪になるようにするパズルだった。 しかし、これがけっこう難しいパズルだと聞いて、著者はその構造を調べてみたくなって、これを借り受けた。 ロープの種類 具体的な板の構成を次に示す。
接し方を考えるとI型は全部で10通り、L型は16通り作れる。その26通りの接し方からなぜこの16種を選んだか、その基準はわからない。 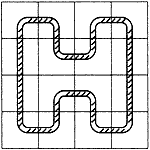 A A
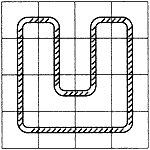 B B
しかし、Bのようにするには、I型の板が8枚必要なので、このセットではAしかできないという結論になる。これで全体の構成がわかったので、それに沿って板を置いて行けばよい。このザイルトリックには、解が220通りある。そのことは、西山輝夫が手計算で、池野信一がコンピュータで、それぞれ独立に確認している。 このザイルトリックは、パズル懇話会の会員に多大の興味を与えた。池野信一は板を20枚に増やし、I型4種とL型の全部(16種)を用いて4×5の長方形に並べて、ロープを輪にするパズルを創案して、「新ザイルトリック」と名付けた。また、六角形のザイルトリックも考案した。これらは『別冊数理科学 パズルIII』(1978年 サイエンス社)に発表されている。 西山輝夫はI型10種、L型16種を全部用いたザイルトリックを創案した。この場合は、4×6の箱の中央に2個分のでっぱりを設ける。興味のある方は、『パズル四重奏α』(サイエンス社)を見られたい。 |
他サイトへの無断転載はご遠慮ください。
●第1部・歴史的なパズル●
- 迷路
- リンド・パピルスのパズル(からす算)
- 魔方陣
- 知恵の輪(チャイニーズリング)
- ヨセフスの問題とまま子立て
- 渡船問題(川渡りの問題)
- 油分け算
- 盗人隠し
- さっさ立て
- 薬師算
- 碁石拾い
- おしどりの遊びと入れ替え問題
- 一小刀問題
- ねずみ算とフィボナッチ数列
- 知恵の板
- 虫食い算
- 目付け字と数当てカード
- 橋渡り問題と一筆書き
- ソリテア
- ハノイの塔
- デュードニー
- サム・ロイド
- 移動板パズル
- 図形消滅パズル
- パラドックス
- 四色問題
- チェスのパズル
- にせ金の問題
●第2部・言葉と絵のパズル●
- 回文
- アナグラム
- 折り句
- 暗号
- ダブレット(変形パズル)
- クロスワードパズル
- サーチワード、クリスクロス
- スクラブル
- 漢字作りパズル
- 単語作りパズル
- 判じ物と判じ絵
- 絵暦
- 新しい単語パズルの作り方
- 電卓文字遊び
- いろいろな文字遊び
- 絵当てパズル
- かくし絵
- さかさ絵
- その他の絵のパズル
●第3部・パズルの展開●
- ポリオミノ
- 立体パズル
- ブラックボックス
- 裏表パズル
- ザイルトリック
- 絵合わせパズル
- 切り継ぎパズル
- お菓子の分配
- クロスワードパズルの数字版
- 電卓数字パズル
- 覆面算
- 年賀用パズル
- コインのパラドックス
- マスターマインド
- パソコン・パズル
- 速算ダイス
- インスタント・インサニティ
- グラスパズル
- 匹見木のパズル
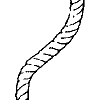 I型
I型
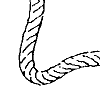 L型
L型
 ロープの接する位置
ロープの接する位置