１−６．渡船問題（川渡りの問題）

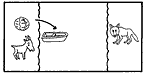
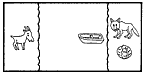
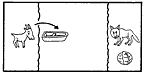
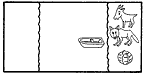
　渡船問題は、東洋では西暦紀元前からあったといわれ、西洋でも８世紀のＡ．アルクインまでさかのぼることができる、きわめて古いパズルである。アルクインの問題は次のようなものである。

　オオカミとヤギを連れ、キャベツのかごを持った男が、川を舟で渡ろうと思った。しかし、舟には男以外にどれか一つしか積むことができない。ところが、男がいないとオオカミはヤギを食うし、ヤギはキャベツを食べてしまう。どうしたら無事に渡れるだろうか。

　この解は２通りあるが、その一つを図解すると[1]のようになる。オオカミとキャベツは一緒に残しても大丈夫だというのが、解くためのヒントである。

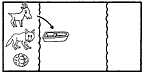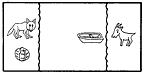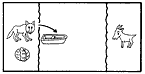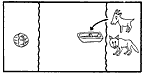　16世紀のタルターリアのものには、次のような問題がある。

　３組の夫婦が川を舟で渡ろうと思った。舟には一度に２人しか乗ることができない。ところが、かれらはきわめて嫉妬深く、妻は自分の夫が対でない他の夫人と一緒にいることは我慢がならない。夫の方も自分の妻が対でない他の男と一緒にいることは許さない。どうしたらトラブルなしに川を渡ることができるだろうか。

　これは11回川を渡る必要がある。[2]は解の一例で、３組の夫をＡ、Ｂ、Ｃで、その妻をａ、ｂ、ｃで表している。

　その後、川の中に島がある問題に進展した。川渡りが無事にできるかどうかは、夫婦の組数と舟の定員によって決まってくる。舟の定員が４人なら、夫婦の組数が何組あっても川渡りが可能である。一組の夫婦が船頭役になって、他の夫婦を一組ずつ対岸に送り届ければよいからである。ボートの定員が２人の場合、川渡りができるのは、夫婦３組までである。しかし、川の中に島があって、そこを中継地点に利用できるなら、４組でも川を渡ることができる。

　渡船問題はさまざまの変種を生んだ。中でも特に有名なのが、「宣教師と人食い人種の問題」である。これも100年くらい前の印刷物にも見ることができるので、けっこう古いパズルである。これもバリエーションがあるが、その一つを紹介しよう。

　３人の宣教師と３人の人食い人が川にさしかかったが、２人乗りの舟が１そうあるだけである。ところで、いかなる時でも、宣教師の数がそこにいる人食い人より数が少なくなると、彼らに殺されしまう。どうしたら無事に渡れるだろうか。

→[答え]