パズルの考え方・解き方（１）

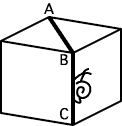
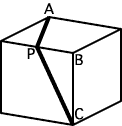
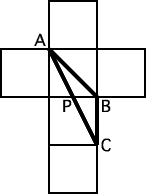
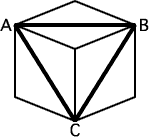
◆パズルとクイズの違い

　パズルというのは、考えもののたぐいを言う。
　これに対してクイズという言葉がある。この二つの言葉は明確に使い分けがされているわけではないが、概してパズルが推理によって解を見いだすのに対して、クイズは知識や機知によって解を得るものを指している。
　パズルの大きな柱は数学パズルと言葉のパズルである。
　数学パズルと呼ばれているものは、数理的に問題を解決するものを指しており、数学と直接は無関係のものも多い。
　言葉のパズルは特に説明は要しないだろう。ただ言葉のパズルには、大なり小なりクイズの要素が含まれている。クロスワード・パズルに至っては、パズルとクイズの要素が半々であると言ってよい。
　これまでに歴史的なパズルや目新しいパズルを紹介してきた。また、そこで問題の解き方等についても可能なかぎり説明したが、とても十分とは言えない。森本清吾はパズルの魅力は解き方が型にはまらず一定でないところにあると言っている。それだけにその解き方も千差万別である。しかし、考え方の基本には共通した点が少なくない。ここでそれをまとめて説明し、本書のまとめとしたいと思う。

◆パズルを解くには即断は禁物、直観に頼るのは危険

　まず、パズルを解く前に注意すべきことは、即断は禁物だということである。見せかけにごまかされてはならない。たとえば[1]では、カタツムリが立方体のＣからＡに向かっているが、どういうコースをとれば最短距離で行くことができるだろうか。ちょっと考えるとＣ→Ｂ→Ａが最短のように見えるが、これは平面的な判断であって立体には通用しない。答は[2]のＣ→Ｐ→Ａのコースである。このことは、[3]のように立方体を展開図にしてみれば明らかだろう。

[1]カタツムリのコースは？

[2]これが最短コース

[3]カタツムリのコースの展開図

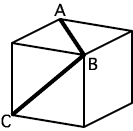
　もう一つ例を挙げよう。[4]の立方体にＡＢ、ＢＣの二本の直線を引いた。この二本の直線がなす角度は何度だろうか。これも即座に90度だと答える人が多い。事実、絵の上ではそう見えるが、これが正解ではない。
　試しにもう一本、ＡＣを結ぶ直線を引いてみよう。立方体の向きを少し変えてみると、[5]になる。これで、はっきりするだろう。ＡＢ、ＢＣ、ＡＣはともに立方体の面の対角線である。したがってその長さは等しい。けっきょく三角形ＡＢＣは正三角形で、ＡＢとＢＣのなす角度は60度である。
　以上、二つの例から明らかなように、パズルを解くのに直観だけに頼るのはきけんである。

[4]２本の直線のなす角度は？

[5]立方体の向きを変える