3−8.お菓子の分配 |
|||
こども向けのパズル・ブックで見かける問題にこんなのがある。 「遊んでいる8人のこどもが、円柱形のお菓子をもらった。これを8人で等分するのに、ナイフを3回入れるだけですましたいのだが、どう切ればいいだろうか。ナイフはまっすぐスパッと切るだけで、回したり、ぎざぎざに切ったりしてはだめだよ」
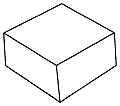
ところで、3人でたとえば右のようなのようなお菓子を分けるのに、最悪でも各人の希望通り、うまくすると全員が得をするという、ちょっと考えられないような巧妙な方法がある。 この分け方は、ポーランドの有名な数学者のH.ステインハウスの著した「数学スナップショット」という本の中に書かれている。 中村義作氏は、チョコレートをコーティングしたお菓子の分配法を考えている。これも大変おもしろいと思う。次のように上の面が正方形をしたケーキがある。このケーキの上面と4側面にはこどもの大好きなチョコレートがコーティングされている。これを5人のこどもに分けようというのだが、分けたお菓子の体積が同じであることはもちろん、チョコレートの塗られている面積も全員同じでないといけない。さあ、どうすればよいだろうか。
そのやり方であるが、まず正方形の2本の対角線を引いて、上面の中心を求める。そうしたら正方形の周囲を5等分して、中心と5等分点とを結ぶ直線を引き、ナイフをこの線に沿って入れて、垂直に切り下ろせばよい。
側面の面積が5つとも等しいことはすぐわかるだろう。上面も正方形の頂点を含む四辺形は、対角線で2つの三角形に分けて考えれば、面積が5等分されていることが理解できると思う。上面の面積が等しければ体積も同じである。このやり方で、一般にn等分することも可能である。 |
他サイトへの無断転載はご遠慮ください。
●第1部・歴史的なパズル●
- 迷路
- リンド・パピルスのパズル(からす算)
- 魔方陣
- 知恵の輪(チャイニーズリング)
- ヨセフスの問題とまま子立て
- 渡船問題(川渡りの問題)
- 油分け算
- 盗人隠し
- さっさ立て
- 薬師算
- 碁石拾い
- おしどりの遊びと入れ替え問題
- 一小刀問題
- ねずみ算とフィボナッチ数列
- 知恵の板
- 虫食い算
- 目付け字と数当てカード
- 橋渡り問題と一筆書き
- ソリテア
- ハノイの塔
- デュードニー
- サム・ロイド
- 移動板パズル
- 図形消滅パズル
- パラドックス
- 四色問題
- チェスのパズル
- にせ金の問題
●第2部・言葉と絵のパズル●
- 回文
- アナグラム
- 折り句
- 暗号
- ダブレット(変形パズル)
- クロスワードパズル
- サーチワード、クリスクロス
- スクラブル
- 漢字作りパズル
- 単語作りパズル
- 判じ物と判じ絵
- 絵暦
- 新しい単語パズルの作り方
- 電卓文字遊び
- いろいろな文字遊び
- 絵当てパズル
- かくし絵
- さかさ絵
- その他の絵のパズル
●第3部・パズルの展開●
- ポリオミノ
- 立体パズル
- ブラックボックス
- 裏表パズル
- ザイルトリック
- 絵合わせパズル
- 切り継ぎパズル
- お菓子の分配
- クロスワードパズルの数字版
- 電卓数字パズル
- 覆面算
- 年賀用パズル
- コインのパラドックス
- マスターマインド
- パソコン・パズル
- 速算ダイス
- インスタント・インサニティ
- グラスパズル
- 匹見木のパズル
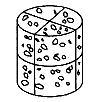 これは平面的に切ろうとしてもだめで、答はむろん右のように切ることである。
これは平面的に切ろうとしてもだめで、答はむろん右のように切ることである。
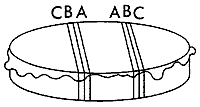
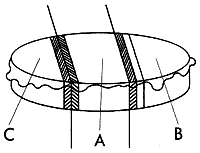
 チョコレートで覆われたケーキを5等分するには?
チョコレートで覆われたケーキを5等分するには?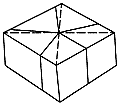 5等分のやり方
5等分のやり方