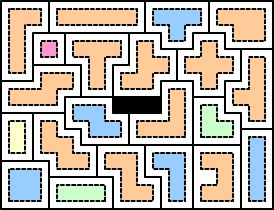
今年２月、パズル仲間の清水敦さんが自身のサイトで「メタボリックペントミノ」というパズルを発表されました。ここで言う「メタボリック」の定義は、あるポリオミノ(正方形を辺同士でつなげた形)の周りを0.5の長さずつ太らせた形のことを言います。上図の点線の形が元の図形です。このメタボリック形は10年以上前、あるパズルを解くのに使用した事があったのですが、それっきりで研究してなく、清水さんの作品を見て先を越されたと思いました。

　では、このメタボリック形を使用したパズルとはどんなものでしょう？　長年パズルをやっていると時々、「ピース同士が接触(点接触も)しないように箱に納めよ」という問題に出合うのですが、この問題は「各ピース同士は１マス以上離して詰めよ」と言い換えることができ、このメタボ形の箱詰めを解けばいいことがわかります。

　ボクの研究対象となるピース、メインはやはり〜５単位までのピースであり、その全てを面積最小の長方形に納めることから始めました。上の図は13×17の長方形で、すき間は３単位あります。これは最小ではないのですが一般のノートの縦横比(１：√２)が好きなので実物はそのサイズで納めています。最小の長方形は11×20で、すき間は２単位になります。

　清水さんの「メタボリックペントミノ」はその名の通りペントミノのメタボリック形を使います。全種を入れることができる最小の長方形に納めるという大変、美しい問題です。

　その問題はどうしてもすき間ができます。それはそれで面白いのですが、ボクはすき間がない問題を考えることにしました。その代わりと言ってはおかしいですが、ほとんどの問題は使わないピースがあります。

最後に調べたQ8で念願のユニーク解(１解)が見つかりました。こりゃ難問だ。
以下、ピースの制約は易しくなりすぎないようにするためです。

※注意：ここでは「Ｕ」のピース（Q9の解例の右上隅のピース）の凹みの向きの違いは別解としていません。

• Q1. １〜５メタボリックオミノ（赤・黄・緑・青・オレンジのピース）で、６×６を作る (16解）
• Q2. ３〜５メタボリックオミノ（緑・青・オレンジ）で、７×７を作る（30解）
• Q3. ４，５メタボリックオミノ（青・オレンジ）で、８×８を作る（16解）
• Q4. ４，５メタボリックオミノ（青・オレンジ）で、９×９を作る（17解）
• Q5. ４，５メタボリックオミノ（青・オレンジ）で、10×10を作る（237解）
• Q6. ４，５メタボリックオミノ（青・オレンジ）で、11×11を作る（８解）
• Q7. ４，５メタボリックオミノ（青・オレンジ）で、12×12を作る（284解）
• Q8. ４，５メタボリックオミノ（青・オレンジ）で、13×13を作る（１解）
• Q9. １，４，５メタボリックオミノ（赤・青・オレンジ）で、14×14を作る（46解）（全て使用）

☆Q9の解例

あと、厚み１で作ると立体問題もできます。

• Q10.メタボ形ＰＴＶｌ(エル)ｏｄｍで８×８を作る（１解）（全て使用）
• Q11.　　　　　 同　上 　　　　　で4×4×4を作る（１解）（全て使用）

ピース名がわからない方は箱詰めパズルの基礎知識を参照してください。

ご意見・ご感想を小田原充宏までお寄せください。