これは構想25年と言っていいかもしれません。20歳の時、ドミノ（目は描かれていない、単なる１×２のピース）をいくつかくっつけたおもしろいパズルを作りたいと思い、木でたくさんのドミノを製作しました。25年の時を経て、それを接着する時が来たのです。
　このパズルを簡単に説明すると、「ドミノだけでつくることができる８×８パズルの中で最もたくさん遊べるもの」となります。

　実は昨年の１月頃、そのドミノピースの接着を開始しました。でもその時はテトロミノを無視していて、最も遊べるヘキソミノ（前までヘクソミノと書いていましたが今回からこの表記にします）12ピースまたは10ピースを選び、６×ｎをつくる問題を解いていったのですが、ピースの多い問題になると難しすぎて一般に販売なんてできないという気持ちが強くなり、しばらく保留していました。

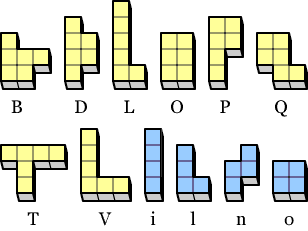
　恥ずかしながら今年４月初め頃、テトロミノも加えたらもっとたくさん遊べるよなぁとようやく気が付いて、ドミノでできるテトロミノ全４種＋使いやすいヘキソミノで考えることにしました。ヘキソミノ８ピースを加えるとちょうど８×８の単位数になるし、４つ子問題（合同形を４つつくる）も可能なので、もうこれ以外考えられません。ヘキソミノの使いやすいベスト８は以前調べた資料に書いてあり、素直にそれを採用すれば良かったのかも知れませんが、今回は敢えてＵの字部分があるものを外しました。理由ですが、「Ｕ」の中の部分は置くことのできるピースが他の隣接部分に比べかなり少ないので、置き方のバリエーションが少ないということと、「Ｕ」の字の部分は、ピースがはまらないということがないようにするのにちょっと手間がかかるという製作上の問題です。

　さきほど、「最もたくさん遊べる」という曖昧な書き方をしましたが、はっきりとした数値で示してほしいという方には、「（厳密には少し違うのですが）８×８の箱に入れるとき、最もたくさんの解があるもの」と思っていただいていいかと思います。これは何と850,135解もあります。もちろん、アソートキューブにはかないませんが。

　８×８パズルで有名なものに「ペントミノ＋ｏテトロミノ」がありますがそれは、アソートヘキサより１ピース多いのに解数は逆に50分の１以下の16,146解しかありません。なぜなら、アソートヘキサが使いやすいピースを選んだものであるのに対し、ペントミノ＋ｏは使いにくいピースが入っているからです。

　アソートヘキサのコンセプトである「ドミノだけでできる形」には、「いくつかのピースを使った問題」がたくさんできるための工夫があって、もしドミノだけでつくることができない偶数オミノがピース群に奇数個入っていたら、すき間のない長方形をつくることができません。なぜ？と思った方は箱詰めパズルの基礎知識の下の方をご覧ください。そんなことで箱詰めが不可能になってしまうようなことがあれば随分、問題数が少なくなってしまいます。というわけでピースは「ドミノだけ」なのです。

　これは盤面を真っ二つにした問題（４×８を２つつくる）が可能です。何とそれが可能なピースの分け方は102通りあり、それを全て問題用紙に収録しました。つまり、４×８に入れる問題は102×２＝204問もあるのです。この４×８というサイズは難しすぎなくて易しすぎないとてもいいサイズです。同時に作ることができるピース群をペアで解数も記載しましたので実力の大きく異なる２人で競争するのにもとても向いています。

　問題用紙には平面が4×5、4×6、5×5（１単位空き）、5×6、6×6の計105問。立体が2×4×4、3×3×4、2×4×5の計43問（全てユニーク解）も収録。さらに、箱への特殊な入れ方（分割線）問題を12問載せました。

ご意見・ご感想を小田原充宏までお寄せください。