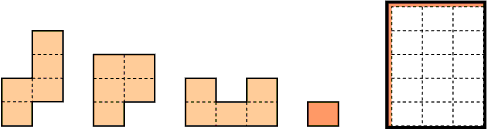
ワンダー16
問１．左側の３ピースをガイド線に従って箱に入れる。
問２．全４ピースを箱に入れる。

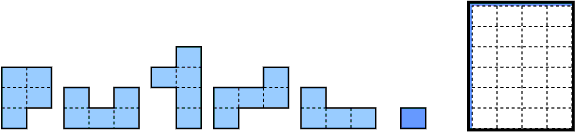
ワンダー25Ｚ
問１．左側の５ピースをガイド線に従って箱に入れる。
問２．全６ピースを箱に入れる。

・・・

いずれもユニーク解。

　今回はパズルの紹介がメインではありません。パズルの魅力を伝えるため、公式を発表します。これを読んだ方がその公式を利用してパズルを作り、楽しんでもらえたらいいと思うわけです。

　まずは上記のパズルについて説明します。
　「ワンダー16」は長方形が５個つながった形が３つで３×５の長方形を作る問題と、それに長方形１つを加えて４×４の長方形を作る問題のどちらもユニーク解になる唯一の駒組です。
　「ワンダー25Ｚ」は長方形が５個つながった形４つと長方形４個をつなげたＬ型１つで４×６の長方形を作る問題と、それに長方形１つを加えて５×５の長方形を作る問題のどちらもユニーク解になる駒組全26通りの中からおもしろそうなものを選びました。

　これらのパズルは中学で習う「(x+1)(x-1) = x²-1」という式を元にしています。
　x に4を代入すると「ワンダー16」。5を代入すると「ワンダー25Ｚ」です。
　この公式をわかりやすく言い換えると、このように縦と横の単位数が同じものから１単位減らすと、その面積は「縦横それぞれ１加えたもの×１減らしたもの」になる。ということです。

　あと、その長方形の縦横比がわからないと作ることはできません。研究の結果、つい最近、その公式を発見したのです。それは「2x-1：2x+1」です。ワンダー16を作りたい場合、１辺は4ですから4を代入するだけです。「７：９」となりましたね。ではこれが正しいか確認しましょう。箱(内寸)のサイズはどちらも４倍なので横28、縦36です。次に縦と横を逆にしたものを計算します。横は「9×(4-1)=27」、縦は「7×(4+1)=35」です。これを比べてください。１ピース余る問題の方が横・縦ともに１だけ短いですよね。
ワンダー25だと９:11、ワンダー36だと11:13、ワンダー49だと13:15、・・・。
　あとはどのように分割するか？が重要ですが「全部を最小単位に分割」でも成り立っているわけで、ピースの大きさや形などの条件を付けさえしなければ易しいので、学校などで誰が考えた分割が難しいか競うのもおもしろいのではないかと思います。

第44回「ワンダーパズル」も参考にしてください。

ご意見・ご感想を小田原充宏までお寄せください。